1.9.1 インピーダンス(IMP)
ボルタンメトリックな方法では、ポテンシャルを特定な範囲内で変化させ、電流応答をモニターします。ボルタンメトリーの1 回の測定では、タイムスケールを一定(例えば、スキャン速度)にします。
IMP 実験では、ポテンシャルは特定な値(例えば、平衡電位)に固定され、小さい振幅のA.C ポテンシャルが重畳されます。1回のIMP 実験であるA.C 周波数範囲が印加され、異なるタイ
ムスケールを有する電気化学的および他の物理的過程が検出できます。
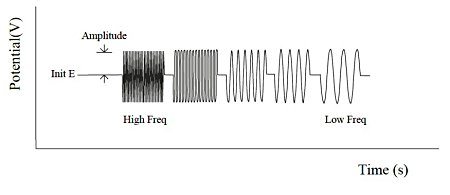
波形発生とデータ解析両方にフーリエ変換法を使います。周波数領域で、1つの周波数と次の周波数の比がほとんど同じで等しい振幅と不規則な位相をもった多数の周波数が選択されます(図39)。この結果周波数が互いに整数倍にならない相対的に等間隔な周波数の1組ができます。
この周波数の1 組は時間領域波形のデジタル表示へ変換され、D/A 変換器とアナログフィルターを経由してセルに印加されます。この手順はS/N 比向上のために多数回繰り返されます。高周波数範囲では、サイクル時間は相対的に短く、実験時間を増やすことなく多数回の積算が実行されます。
それぞれの周波数範囲で感度が自動的に調節した電流応答がモニターされます。各周波数範囲の測定が終了すると、データはフーリエ変換アルゴリズムによって解析されます。実験データの表現は印加ポテンシャルと電流応答間の位相差により複雑になります。結果はインピーダンス(Z = E /I)或いはアドミッタンス (Y =1/ Z)として表わされます。
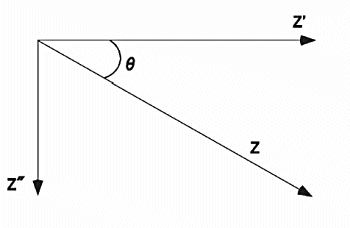
Z(トータルインピーダンス)、Z '(印加電圧と同相インピーダンス),Z"(印加電圧90゜位相のインピダーンス)とθ(位相角)間の関係をあらわす図を図40 に示します。これらの変数は周波数(ω)とともに変化することにご注意下さい。
プロットできるデータの種類
- Nyquist: -Z"-Z'
- Bode: LogZ & phase - Log(Freq)
- LogZ - Log(Freq)
- phase - Log(Freq)
- log(Z’& Z”) - Log(Freq)
- logY - log(Freq)
- Admittance: Y”- Y’
- Warburg: Z" & Z' - 1/sqrt(w)
- Z’- wZ”
- Z' - Z"/w
- Cot(phase)-Sqrt(w)
- 1/wZ” - 1/wZ’
- Y"/w-Y'/w
インピーダンス測定の最も難しい面の1つは実験データの解釈です。基本的な考え方は電気化学セルを電子回路の等価回路でおきかえられるというところにあります。 例えば、界面領域は静電容量Cdl のコンデンサーに似ています。また作用電極と参照電極間の未補償溶液抵抗Ru があります。モデル化した電気化学セルの他の構成要素には電子移動(ファラデーインピーダンス)と拡散物質移動(Warburgインピーダンス)を含みます。
ファラデーインピーダンスの理論的裏づけは次のようになります。もし印加電圧(A.C 振幅)が小さい(約5/n mV, nは移動電子数)ならば、印加電圧と電流応答間は直線関係です。即ち、I=E/Rfとなり、Rf はファラデーインピーダンスです。
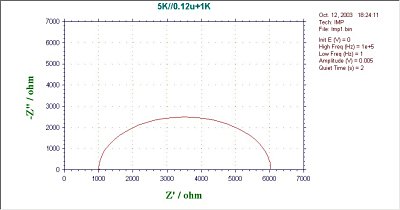
Rf は電子移動速度の逆数に比例します。小さい方の切片はZ'=Ru 、大きい方の切片はZ'= Ru +Rf になります。半円形の最大-Z" 値に対応する周波数は1/RuCdl に等しくなります。従って、この簡単なRC回路の3つの構成要素はインピーダンス測定から算出されます。
Nyquist プロットは一般的に最も多くのデータ表示に使われる方法です。Bode プロットは Nyquistプロットより分解能が良いので、もし系を支配する過程が1 つ以上ならば、有用です。インピーダンスプロットは多くの情報が得られますが、非常に複雑であり、説明するのが難しいことがあります。
例えばNyquistプロットでは、1つ以上の半円が存在することがありますし、正の象限にないことが多いのです 。インピーダンス測定は広く電子移動速度の研究、例えば、腐食やバッテリーの研究に使用されてきました。また、電極表面上の電気化学活性ポリマーフィルムを流れる電子の移動速度を測定するために使用されています。