2.4.くし形電極を用いた高感度ボルタンメトリ
図3はくし形電極を用いたフェロセンのサイクリックボルタモグラムである。
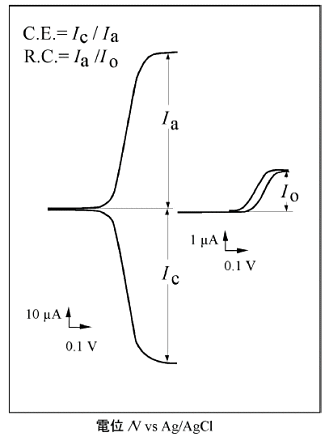
Aは一方の電極( C極) を還元電位に固定し、もう一方の電極( G極) の電位を走査した時の2つの電極での電流を酸化電流を正として同時に記録したものである(GCモード)。B図2. レドックスサイクルの概念図はC極に電位を印加せずに走査した場合の、通常のサイクリックボルタモグラムである(O モード)。
Aでは0. 4V 付近からG極での酸化電流が増加しはじめ、それに応じてC極での還元電流が増加し、0.6V 付近でどちらも一定になり絶対値が同じ程度の電流となっている。
この酸化電流に対する還元電流の割合は捕捉率と呼ばれ、G極で発生した酸化体がどのくらいC極に到達するかを示している。
微小くし形電極を用いたボルタンメトリでは90%以上の高い捕捉率が得られる。一方、C 極に電位を印加しない場合、レドックスサイクリングが生じないため、通常の拡散律速に基づく応答となり、G極の電流値 Io は小さくなる。
そこで C極に電位を印加した際の電流値 Ia との比をレドックスサイクリング数と定義し、見かけの電流増加の割合を比較する指標とした。
図4は電極幅やギャップの異なるくし形電極における限界電流を(5) 式に従ってプロットしたもので、実線の理論値とよく一致しており、理論の有効性と共に、この方法による定量的分析が可能であることを示している。
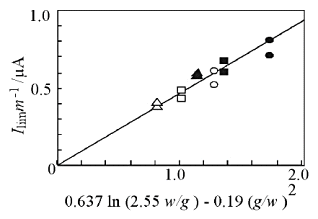
さらに、拡散係数の異なるレドックス種に対する捕捉率およびレドックスサイクリング数を検討したところ、いずれもレドックス種によらず、電極形状のみで決まっていることがわかった。
図5に4種の可逆な活性種についてレドックスサイクリング数の形状依存性を示す。特に電極を微細化した際、レドックスサイクリング数が急激に増加しており、サイクル数の増加と共に限界電流も増加する。これは微細化による高感度化が有効であることを示唆している。