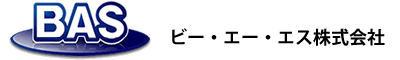トップページ > 電気化学計測 > これから電気化学を始める方のための基礎 > 電気化学インピーダンス分光法（EIS）について

電気化学測定法である電気化学インピーダンス分光法（EIS）についての基礎的な内容です。
その他はこちら

電気化学インピーダンス分光法(EIS)について(7)：ネルンスト拡散

拡散の特殊なケース　ここまで考えてきた拡散（ワールブルグ拡散）は半無限一次元拡散の境界条件が成り立つ場合でした。それでは半無限一次元拡散の境界条件が成り立たない場合はどうなるのか。例えば、修飾電極中の活物質の移動や色素増感型やペロブスカイト型太陽電池などの場合のように電子やイオンの移動範囲が限定される拡散、回転電極のような定常的な拡散層が形成されるような場合などである。このような拡散に対してはいくつか異なる取り扱いが行われています。それぞれについて分けて述べましょう。
最初はネルンスト拡散モデル（Nernst diffusion, ND）と呼ばれるものです。移動が限定される場合で、有限拡散モデル（finite diffusion, FD）と呼ばれる場合もあります。有限厚さの拡散層は存在するが、移動が限定されないもので、回転電極やプロトン交換膜型燃料電池（PEMFC）がND拡散に対応します。NDのインピーダンスは下式で与えられる。

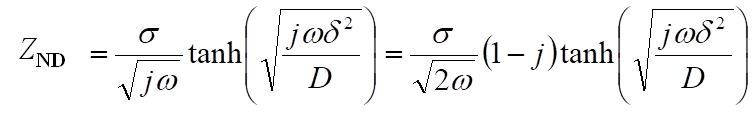
ここでσはワールブルグインピーダンス中（このシリーズの4回目）に表れるものと同じものです（活物質の濃度や拡散係数の値に依存し、これらが大きくなるとσは減少、従ってインピーダンスも減少します）。δは膜厚に相当するものです。式から比δ2/Dによってプロファイルが影響されるとともに、活物質濃度Cもσに大きな影響を及ぼすので、これらC、D、δによって複雑に変化する。δが増えると直線部分が長くなる。CやDが減少すると拡散インピーダンスが大きくなるがCの効きかたの方が大きい。
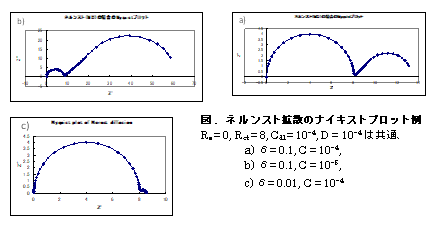
この式のシミュレーション例を下図に示します。Rs＝0、Rct＝8、Cdl＝10-4、D＝10-4として、濃度Cと膜厚δに対するパラメータを変化させたときのナイキストプロットの変化を示したものです。