トップページ > 電気化学計測 > これから電気化学を始める方のための基礎 > 電気化学インピーダンス分光法(EIS)について
電気化学測定法である電気化学インピーダンス分光法(EIS)についての基礎的な内容です。
その他はこちら
色素増感太陽電池(DSSC)に用いられるナノ粒子TiO2膜アノードは等価回路的には分布定数回路、あるいは伝送線モデルで表すのが優れている(図1)。上側ラインのrtは酸化チタン粒子中の電子の移動速度からくる抵抗成分の微分的寄与、下側ラインは溶液側の抵抗だが微分的寄与は小さいとして無視する。
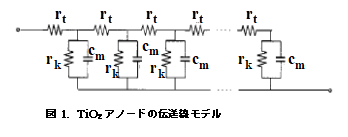
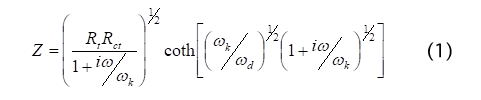
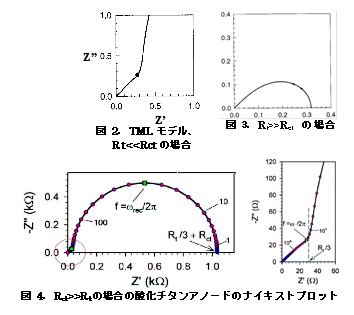
図2は高周波数部を拡大して表したものである。全体を示すと図4になる。特徴は高周波数部における勾配45度の直線とそれに続く中間周波数から低周波数部にかけての一つのアークである。アークの頂点周波数(ωrec/2π)、f=0におけるインピーダンス(直流抵抗値,Rt/3 + Rct)、高周波数部の直線とアークの交点の実軸(Rt/3)の値からRct、Rt、Cmの値が求められる。Rtはメソポーラス酸化チタン電極中の電子移動に関わる抵抗であり、できるだけ小さいことが望ましい。Rct(またはRrec)は酸化チタン電極中の電子の再結合反応(主として電解液中のI3-の還元に消費される)抵抗で、再結合反応が遅いほどRctは大きくなり、DSSCとしては望ましい。CmはTiO2に注入される電子量が反映されるので大きいことが望まれる。
電気化学測定法である電気化学インピーダンス分光法(EIS)についての基礎的な内容です。
その他はこちら
- その7:電気化学インピーダンス分光法(EIS)について(1):等価回路によるEIS結果解析の基本
- その7:電気化学インピーダンス分光法(EIS)について(2):周波数変化とEIS測定
- その7:電気化学インピーダンス分光法(EIS)について(3):回路素子のナイキストプロット
- その7:電気化学インピーダンス分光法(EIS)について(4):ワールブルクインピーダンス
- その7:電気化学インピーダンス分光法(EIS)について(5):CPEのナイキストプロット
- その7:電気化学インピーダンス分光法(EIS)について(6):3つの素過程からなる系を考える
- その7:電気化学インピーダンス分光法(EIS)について(7):ネルンスト拡散
- その7:電気化学インピーダンス分光法(EIS)について(8):有限拡散
- その7:電気化学インピーダンス分光法(EIS)について(10):色素増感太陽電池(DSSC)のEIS-2
- その7:電気化学インピーダンス分光法(EIS)について(11):まとめ
電気化学インピーダンス分光法(EIS)について(9):色素増感太陽電池(DSSC)のEIS-1

上下をつなぐ並列回路はナノ粒子/溶液界面における電子の再結合反応速度に相当する抵抗成分の微分的寄与rkと、界面二重層容量およびケミカルキャパシタンス(酸化チタン粒子中に注入された電子密度の変化に対応する)の合わさった容量の微分的寄与cmからなる。このモデルのインピーダンスは(1)式で与えられる。
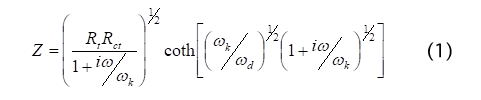
TiO2薄膜電極の厚さをLとすると
- Rt=rtL
- Rct=rk/L
- Cm=cmL
- ωk=1/CmRct
- ωd=1/CmRt
の関係がある。
Rt<<Rctのとき、Z=(Rt/3)+[Rct/{1 + (iω/ωk)}]が成り立ち、ナイキストプロットは図2のようになる。一方、Rt>>Rctの場合はZ=[RtRct /{1 + (iω/ωk)}]1/2が成り立ち、図3のようになる。DSSCとしてはRctがうんと大きな(つまり注入された電子の再結合が少ない)図2の方が望ましい。

RctCmは低周波域の半円の時定数であり、この値が大きいことは半円ができるだけ低周波数に現れ、かつその半円の径が大きいことである。抵抗値が大きく、半円が大きなほど良いというのは奇異に思われるかもしれないが再結合反応速度が遅いほどロスが少なくDSSCが有効に機能するためである。Bisquertらのグループにより開発、発展された手法であるが1)最近、俄かに注目されているペロブスカイト型SCの解析にもこの手法が適用可能である。
1) 関連文献は沢山あるが一例として J. Bisquert et al., J. Am. Chem. Soc., 130, 11312, (2008)